When analyzing data, understanding the strength and direction of the relationship between two variables is crucial. The Spearman correlation, a non-parametric measure of rank correlation, is particularly useful in this context. Let me walk you through the process of calculating Spearman correlation in Excel.
Key Takeaways:
- Spearman correlation evaluates rank-based relationships, making it suitable for non-linear or ordinal data.
- The process involves ranking data, calculating rank differences, squaring them, and applying a specific formula.
- It is effective for non-linear relationships and is resilient to outliers.
- Applications of Spearman correlation extend to fields like psychology, finance, healthcare, and environmental studies.
Table of Contents
Utilizing Data Relationships with Spearman Correlation
What is Spearman Correlation?
Spearman correlation, also referred to as Spearman’s rank correlation coefficient, is a non-parametric measure that evaluates the strength and direction of the association between two variables. Unlike Pearson correlation, which assumes data to be linear and normally distributed, Spearman correlation focuses on ranked data, making it perfect for ordinal data or non-linear relationships.
Understanding the Importance of Ranking Data
In statistical analysis, comprehending the relationships between different data sets is essential. Spearman’s rank correlation coefficient provides insight into these relationships by concentrating on the ranks rather than the raw data. This method is especially beneficial when dealing with ordinal or non-parametric data, where the magnitude of the difference between data points is less important than their order.
For instance, if you are analyzing customer satisfaction ratings in relation to wait times at a restaurant, the actual scores may differ, but Spearman correlation focuses on whether a higher wait time consistently correlates with a lower satisfaction ranking, irrespective of the numerical values.
Steps to Compute Spearman Correlation in Excel
Prepare Your Data
First, ensure that your dataset is organized into two columns—one for each variable you wish to analyze. For example:

Rank the Data
To perform Spearman correlation, you need to rank the values in each variable. Utilize Excel’s RANK.AVG function for this purpose:
Rank Variable X: In a new column, apply the formula:
=RANK.AVG(A2, A$2:A$6, 1)

Rank Variable Y: In another column, use the formula:
=RANK.AVG(B2, B$2:B$6, 1)

You should now have ranked data for both variables.
Calculate the Difference Between Ranks
Create a column for the difference (Δ) between the ranks of each variable:
=D2 – C2

Square the Differences
Create another column to square the differences (Δ2):
=(E2)^2

Sum the Squared Differences
At the bottom of the Δ2 column, use the SUM function to calculate the total sum of squared differences (∑Δ2):
=SUM(F2:F6)

Apply the Spearman Correlation Formula
The formula for Spearman correlation (ρ) is:

This will yield the Spearman correlation coefficient.
Interpreting the Result
The Spearman correlation coefficient ranges from ?1 to 1:
- 1: Perfect positive correlation.
- 0: No correlation.
- ?1: Perfect negative correlation.
A coefficient closer to 1 or ?1 indicates a strong relationship, while a coefficient near 0 suggests a weak or no relationship.
Employing Excel’s Data Analysis ToolPak
If manual calculations seem overwhelming, you can utilize the Analysis ToolPak add-in for statistical computations. Unfortunately, Excel does not have a built-in Spearman correlation function, but you can compute Pearson correlation on ranked data to obtain the same result.
STEP 1: Rank Your Data by following the steps mentioned above.

STEP 2: Use the CORREL function to get the correlation coefficient.
=CORREL(C2:C6,D2:D6)

This will give you the Spearman correlation coefficient.
Enhancing Your Skills: Spearman Correlation in Practice
Real-world Applications Where Spearman Makes a Difference
Spearman correlation is a versatile tool with significant impacts across various fields. Let’s explore a few real-world applications where Spearman correlation proves advantageous:
- In psychology, Spearman correlation assists in analyzing questionnaire data where responses are ranked on a Likert scale, revealing monotonic relationships between variables like stress and sleep quality.
- In education, it can reveal correlations between students’ rankings in different subjects, such as mathematics vs. natural sciences, providing insights for curriculum development.
- In finance, it is used to understand the relationship between the rank order of stock prices over different periods, which is crucial for portfolio management.
- In healthcare, Spearman correlation might correlate patient satisfaction rankings with hospital readmission rates, offering valuable feedback for hospital administrators.
- Environmental studies often use Spearman to explore the relationship between the ranked order of pollutant levels and the incidence of certain diseases within a population.
These examples demonstrate Spearman’s capability to decipher rank-based relationships, providing clarity even when data distributions are unconventional or non-linear. By employing Spearman correlation, professionals in these fields can derive insights that inform decisions, drive policy changes, and shape strategic directions.
FAQ: Mastering Spearman Correlation in Excel Made Simple
How to compute Spearman correlation?
To compute Spearman correlation in Excel: Rank both data sets, find the difference between each pair of ranks, square those differences, sum all squared differences, and use the formula rs = 1 – (6 * Σd^2) / (n * (n^2 – 1)), where Σd^2 is the sum of squared rank differences, and n is the number of observations.
What are the benefits of using Spearman correlation over Pearson correlation?
Spearman correlation is more robust than Pearson as it does not require assumptions of normality and linearity, making it ideal for ordinal data, non-linear relationships, or when outliers are present that could skew Pearson results.
How do I handle tied ranks when calculating Spearman correlation in Excel?
In Excel, use the RANK.AVG function to handle tied ranks, which assigns each tied value the average of the ranks they would cover; this ensures tied data points are assigned their proper rank, crucial for the accuracy of Spearman correlation.
Can Spearman correlation be used for non-linear relationships?
Yes, Spearman correlation is suitable for non-linear relationships because it assesses the monotonic relationship based on rank rather than the absolute values, making it ideal for data that does not fit a linear model.
What does a Spearman correlation coefficient close to zero signify?
A Spearman correlation coefficient close to zero signifies that there is no apparent monotonic relationship between the ranked variables; the ranks do not consistently increase or decrease together.
? ??? Excel? Spearman ?? ??? ?? ??? ? ??? – ?? ?? ???? ?? ?????. ??? ??? PHP ??? ????? ?? ?? ??? ?????!

? AI ??

Undress AI Tool
??? ???? ??

Undresser.AI Undress
???? ?? ??? ??? ?? AI ?? ?

AI Clothes Remover
???? ?? ???? ??? AI ?????.

Clothoff.io
AI ? ???

Video Face Swap
??? ??? AI ?? ?? ??? ???? ?? ???? ??? ?? ????!

?? ??

??? ??

???++7.3.1
???? ?? ?? ?? ???

SublimeText3 ??? ??
??? ??, ???? ?? ????.

???? 13.0.1 ???
??? PHP ?? ?? ??

???? CS6
??? ? ?? ??

SublimeText3 Mac ??
? ??? ?? ?? ?????(SublimeText3)
 Excel Pivot ????? ??? ????? ??
Jul 11, 2025 am 01:01 AM
Excel Pivot ????? ??? ????? ??
Jul 11, 2025 am 01:01 AM
Excel Pivot ???? ??? ?????? ??? ???? ????? ??? ??? ?? ?? ???? ?? ? ?? ?? ??? ?? ? ?? ????? ??? ????? ???? "Month"??? ???????. ??? ???? ?? ?? ???? ??? ??? ????? ???? ?? ???? ????? ?? ??? ??????.
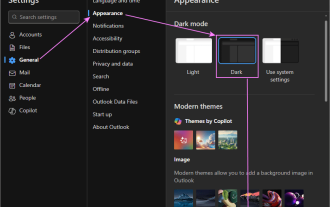 Outlook? ??? ??? ???? ?? ??
Jul 12, 2025 am 09:30 AM
Outlook? ??? ??? ???? ?? ??
Jul 12, 2025 am 09:30 AM
???? ??? Outlook ?? ?????? Light and Dark Mode? ???? ??? ?? ? ??? ?? ?? ?? ???? ??? ?????. ?? ?? ???? ?? ???? Outlook Dark Mode? ?? ??? ???
 Excel? ?? ? ? ?? ????? ?? ?? ???? ??
Jul 09, 2025 am 02:24 AM
Excel? ?? ? ? ?? ????? ?? ?? ???? ??
Jul 09, 2025 am 02:24 AM
Excel? ?? ? ? ??? ? ?? ??? ????? "Top Title Row"??? ??????. ?? ?? : 1. Excel ??? ?? "??? ????"?? ??????. 2. "?? ??"??? ?????. 3. ?? ??? "?? ?? ?"? ???? ?? ? ?? (? : 1 ?)? ??????. 4. "??"? ???? ??? ??????. ?? ?? ?? : ???? ?? ?? ?? ? ?? ?? ?? ??, ??? ??? ??? ??? ?? ?? ?? ??? ??? ???? ????. ?? ?? ??? ??? ?????? ExcelOnline ?? ??? ???? ??? ?? ??? ????? ?????? ?? ????.
 Windows PC?? ??? ? ?? : Windows 10 ? 11
Jul 23, 2025 am 09:24 AM
Windows PC?? ??? ? ?? : Windows 10 ? 11
Jul 23, 2025 am 09:24 AM
PC?? ??? ?? ?? ?? ??????. ?? ??? ???? ?? ?? ???? ?? ? ? ????. ?? ??? ??? PRT SC ??? ???? ?? SCRN ?? (?? ?? ?)? ??? ????. ??????
 ?? ??? ???? ?? ???? ??????
Jul 09, 2025 am 01:53 AM
?? ??? ???? ?? ???? ??????
Jul 09, 2025 am 01:53 AM
MicrosoftTeamsRecordingSareStoredIntheCloud, ????? indriveorsharePoint.1. RecordingSussusSustualsSubleStotheInitiator'SonEdriveina“Recordings”?? ??“Content.”2. FilesMayGotOtheOrganizer'SonEdRiveOpoIntSiteLointELEDELEDETELEDETELEDOPOPOINTSINTELOINTERMEETSORWWEBINARS
 Excel?? ? ??? ? ?? ?? ??
Jul 08, 2025 am 01:09 AM
Excel?? ? ??? ? ?? ?? ??
Jul 08, 2025 am 01:09 AM
Excel?? ? ??? ? ?? ?? ?? ? ???? ??? ? ????. ??? = ? (??, 2)??, ??? ??? ??? ?????. ?? ?? ????? ???? ?? ?? ?? ???? ? ?? ?? ?? ??? ?? ?? = max (if (rangemax (??)))? ??? ? ??? Ctrl Shift Enter? ?? Excel? ?? ??? ???????. ??? ???? ?? ???? ?? ???? ?????? ???? ? ?? ?? ?? ???? ?? ? ?? ???? ??? ?? ???? ??? ?????. ?? ???? ?? ? ?? ???? ?? ????.
 Web?? ???? Excel? ?? ?? ??
Jul 11, 2025 am 01:02 AM
Web?? ???? Excel? ?? ?? ??
Jul 11, 2025 am 01:02 AM
TopullDataFromthewebintoExcelwithOutCoding, usePowerQueryForStucturedHtMltMltBableStablesTABLEDATATINGEDATA> getData>?? webandselectingThedesiredTable; theMethodWorkSbestForStaticContent.ifthesiteOffersxMlorJSonFeeds, ImportTheMviaPiApeoryBiAnter