Software Tutorial
Software Tutorial
 Office Software
Office Software
 How to Use Pythagorean Theorem in Excel – Step by Step Formula Guide
How to Use Pythagorean Theorem in Excel – Step by Step Formula Guide
How to Use Pythagorean Theorem in Excel – Step by Step Formula Guide
May 16, 2025 pm 05:45 PMThe Pythagorean Theorem is an essential mathematical concept that frequently proves its utility across various projects, from distance calculations to practical constructions. Incorporating this theorem into Excel has significantly streamlined my work, saving me hours. Let me guide you through my method of utilizing Excel for Pythagorean Theorem calculations.
Key Takeaways:
- Excel simplifies calculations involving the Pythagorean Theorem with functions such as SQRT and exponentiation.
- A well-organized spreadsheet layout ensures precision and user-friendliness in triangular calculations.
- Excel's formulas can be adapted to determine not only the hypotenuse but also other triangle sides.
- The Law of Cosines expands Excel's utility to non-right triangles, enhancing its mathematical applications.
- Employing error handling functions like IFERROR can aid in resolving formula errors and improve efficiency.
Table of Contents
Exploring the Pythagorean Theorem in Excel
Understanding the Pythagorean Theorem
A quick refresher on the theorem: it declares that in a right triangle, the square of the hypotenuse ("c") equals the sum of the squares of the other two sides ("a" and "b"). The formula is expressed as:
c2 = a2 b2
To solve for the hypotenuse, rearrange the formula to:
c = √(a2 b2)
Excel streamlines this calculation, making it unnecessary to resort to manual computations.
Excel: A Powerful Ally in Problem Solving
Excel extends beyond financial analysis; it's an invaluable tool for mathematicians and educators. Its grid structure resembles graph paper, perfect for visualizing and tackling mathematical issues, including those involving the Pythagorean Theorem. Excel's cell references and built-in functions facilitate dynamic calculations that adjust automatically as input values change.
This functionality is especially beneficial for analyzing multiple scenarios or conducting what-if analyses. By leveraging Excel's capabilities, solving intricate mathematical problems like determining the length of the hypotenuse or the legs of right-angled triangles becomes a structured and engaging experience for students and professionals alike.
Quick Guide: Utilizing the Pythagorean Theorem in Excel
Setting Up Your Excel Spreadsheet for Triangular Calculations
To prepare an Excel spreadsheet for triangular calculations, follow a series of deliberate steps that promote accuracy and ease of use. Start by designing a clear layout. Label columns for the different sides of the triangle—typically 'a,' 'b,' for the legs, and 'c' for the hypotenuse. Enter known values into the respective cells.

For multiple triangles, distinguish between each set of values—using separate rows can help. Reserve cells for displaying calculation results, and consider using color-coding or bolding these for quick reference. Ensure the spreadsheet uses the correct unit of measurement that aligns with the data you'll input.
Enter the Formula: Calculating Hypotenuse and Legs Easily
To easily calculate the length of the hypotenuse, utilize Excel's SQRT and exponentiation (^) functions. Assume cells A2 and B2 hold the lengths of the legs 'a' and 'b,' respectively. In cell C2, reserved for the hypotenuse 'c,' enter the formula "=SQRT(A2^2 B2^2)".

Excel immediately squares both values, sums them, and calculates their square root, providing the length of the hypotenuse.
To reverse the process and find one of the legs when the hypotenuse and the other leg are known, slightly modify the formula to subtract the square of one leg from the square of the hypotenuse before taking the square root.
a = √(c2 – b2)

For accuracy and to prevent errors, use parentheses to correctly group the operations.
Advanced Uses of the Pythagorean Theorem in Excel
Handling Non-Right Triangles: Excel's Continued Support
Even when dealing with non-right triangles, Excel remains a valuable tool. While the Pythagorean Theorem applies only to right-angled triangles, Excel can assist with non-right triangles by using the Law of Cosines, an extension of Pythagorean principles.
For a triangle with sides 'a,' 'b,' and 'c,' and an angle 'C' opposite side 'c,' the formula "=SQRT(A2^2 B2^2 – 2A2B2*COS(RADIANS(C2))" calculates the length of side 'c.' Substitute A2, B2, and C2 with the appropriate cell references and angle measurements.

Excel's ability to incorporate trigonometric functions like COS showcases its versatility beyond basic Pythagorean Theorem applications. Remember to convert angles to radians using the RADIANS function within Excel.
Resolving Common Issues with the Pythagorean Theorem in Excel
Deciphering Error Messages: Understanding Excel's Feedback
Understanding Excel's error messages is key to maintaining workflow and ensuring precise calculations. Common errors like #VALUE! often indicate a non-numeric input where a number was expected; verify that all side lengths are numeric.

A #NUM! error suggests a problem with a formula, such as attempting to take the square root of a negative number when calculating a triangle side—ensure your triangle dimensions are geometrically valid.
The #DIV/0! error signals a division by zero, which shouldn't occur in Pythagorean calculations but might arise from using the wrong formula.
For effective error handling, use Excel's IFERROR function to specify an alternative result or message when an error is detected.
Ensuring Accuracy: Verifying Data Entry and Formula Application
Accuracy in Excel's Pythagorean calculations involves checking both data entry and formula application. To avoid common errors, always verify the entered side lengths against source data. Watch out for accidental spaces or non-numeric characters that can lead to errors or incorrect results.
For formulas, ensure each part is in the correct sequence and that parentheses are correctly used to structure calculations. Utilize Excel's "Trace Precedents" and "Trace Dependents" features to visualize formula relationships and data flow. For added assurance, I always perform spot checks with manual calculations or a secondary reliable method. Cross-referencing results boosts confidence in the spreadsheet's accuracy.
Optimizing Excel for Improved Pythagorean Calculations
Exploring Excel's Functions and Formulas: Enhancing Capabilities
Diving deeper into Excel's arsenal of functions, I often discover various tools that can be creatively applied to Pythagorean calculations. Beyond basic arithmetic operators, functions like POWER (for squaring values) and ABS (for handling absolute values) help refine formula construction.
For instance, rather than using the caret (^) for exponentiation, I can use "=SQRT(POWER(B5,2) POWER(C5,2))" to calculate the hypotenuse.

This approach is particularly effective for complex formulas, enhancing clarity and precision. Excel also supports the creation of custom formulas, allowing the entire Pythagorean process to be encapsulated into a single, reusable function—a pinnacle of its capabilities that can save significant time.
Tips and Techniques: Enhancing Efficiency in Pythagorean Calculations with Excel
Keyboard Shortcuts and Productivity Hacks for Faster Results
In my pursuit of efficiency, mastering Excel's keyboard shortcuts has transformed my work with the Pythagorean Theorem. Shortcuts like Ctrl C for copying, Ctrl V for pasting, and Ctrl Z for undoing actions are just the beginning. To quickly enter and edit formulas, I use F2 to edit the active cell, and Ctrl Shift Enter to input array formulas, which are invaluable for handling complex data sets.
For frequently used functions like SQRT, creating named ranges and using the Name Manager saves clicks and typing time. Additionally, customizing the Quick Access Toolbar to include the most-used tools places them right at my fingertips, further speeding up my workflow. Adopting these productivity hacks leads to faster results and turns the user experience from labor-intensive to efficient and enjoyable.
FAQ: Excelling at the Pythagorean Theorem in Excel
How to implement the Pythagorean Theorem in Excel?
To implement the Pythagorean Theorem in Excel, input the lengths of two sides of a right-angled triangle and use the formula a^2 b^2 = c^2 in a cell. For the hypotenuse 'c', enter "=SQRT(A2^2 B2^2)" assuming 'A2' and 'B2' contain the side lengths. Excel calculates the square root of the sum of squares, yielding the length of the hypotenuse.
Can Excel be used to find missing triangle sides other than the hypotenuse?
Yes, you can rearrange the formula to find a missing leg by using "=SQRT(C5^2 - B5^2)", where C5 is the hypotenuse and B5 is the known leg.
How can I ensure my Pythagorean calculations are accurate in Excel?
Double-check data entry, use parentheses correctly in formulas, and cross-verify with manual calculations or another tool. Excel's "Trace Precedents" feature also helps visualize formula dependencies.
What should I do if I encounter an error when calculating the hypotenuse?
A #VALUE! error usually means a non-numeric input, while a #NUM! error could indicate an invalid square root operation. Use IFERROR to handle errors gracefully.
Can Excel perform calculations for non-right triangles?
Yes, you can use the Law of Cosines formula in Excel: "=SQRT(A2^2 B2^2 - 2A2B2*COS(C2))", ensuring the angle is in radians by using the RADIANS function.
The above is the detailed content of How to Use Pythagorean Theorem in Excel – Step by Step Formula Guide. For more information, please follow other related articles on the PHP Chinese website!

Hot AI Tools

Undress AI Tool
Undress images for free

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Clothoff.io
AI clothes remover

Video Face Swap
Swap faces in any video effortlessly with our completely free AI face swap tool!

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 How to Use Parentheses, Square Brackets, and Curly Braces in Microsoft Excel
Jun 19, 2025 am 03:03 AM
How to Use Parentheses, Square Brackets, and Curly Braces in Microsoft Excel
Jun 19, 2025 am 03:03 AM
Quick Links Parentheses: Controlling the Order of Opera
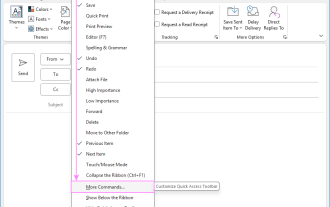 Outlook Quick Access Toolbar: customize, move, hide and show
Jun 18, 2025 am 11:01 AM
Outlook Quick Access Toolbar: customize, move, hide and show
Jun 18, 2025 am 11:01 AM
This guide will walk you through how to customize, move, hide, and show the Quick Access Toolbar, helping you shape your Outlook workspace to fit your daily routine and preferences. The Quick Access Toolbar in Microsoft Outlook is a usefu
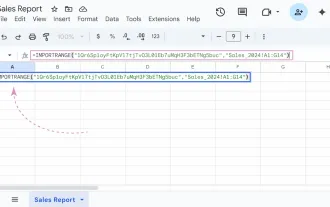 Google Sheets IMPORTRANGE: The Complete Guide
Jun 18, 2025 am 09:54 AM
Google Sheets IMPORTRANGE: The Complete Guide
Jun 18, 2025 am 09:54 AM
Ever played the "just one quick copy-paste" game with Google Sheets... and lost an hour of your life? What starts as a simple data transfer quickly snowballs into a nightmare when working with dynamic information. Those "quick fixes&qu
 6 Cool Right-Click Tricks in Microsoft Excel
Jun 24, 2025 am 12:55 AM
6 Cool Right-Click Tricks in Microsoft Excel
Jun 24, 2025 am 12:55 AM
Quick Links Copy, Move, and Link Cell Elements
 Don't Ignore the Power of F9 in Microsoft Excel
Jun 21, 2025 am 06:23 AM
Don't Ignore the Power of F9 in Microsoft Excel
Jun 21, 2025 am 06:23 AM
Quick LinksRecalculating Formulas in Manual Calculation ModeDebugging Complex FormulasMinimizing the Excel WindowMicrosoft Excel has so many keyboard shortcuts that it can sometimes be difficult to remember the most useful. One of the most overlooked
 Prove Your Real-World Microsoft Excel Skills With the How-To Geek Test (Advanced)
Jun 17, 2025 pm 02:44 PM
Prove Your Real-World Microsoft Excel Skills With the How-To Geek Test (Advanced)
Jun 17, 2025 pm 02:44 PM
Whether you've recently taken a Microsoft Excel course or you want to verify that your knowledge of the program is current, try out the How-To Geek Advanced Excel Test and find out how well you do!This is the third in a three-part series. The first i
 How to recover unsaved Word document
Jun 27, 2025 am 11:36 AM
How to recover unsaved Word document
Jun 27, 2025 am 11:36 AM
1. Check the automatic recovery folder, open "Recover Unsaved Documents" in Word or enter the C:\Users\Users\Username\AppData\Roaming\Microsoft\Word path to find the .asd ending file; 2. Find temporary files or use OneDrive historical version, enter ~$ file name.docx in the original directory to see if it exists or log in to OneDrive to view the version history; 3. Use Windows' "Previous Versions" function or third-party tools such as Recuva and EaseUS to scan and restore and completely delete files. The above methods can improve the recovery success rate, but you need to operate as soon as possible and avoid writing new data. Automatic saving, regular saving or cloud use should be enabled
 5 New Microsoft Excel Features to Try in July 2025
Jul 02, 2025 am 03:02 AM
5 New Microsoft Excel Features to Try in July 2025
Jul 02, 2025 am 03:02 AM
Quick Links Let Copilot Determine Which Table to Manipu