Understanding Algorithm Efficiency: A Comprehensive Guide
Have you ever wondered why some algorithms outperform others? The answer lies in their time and space complexity. Time complexity measures the execution time relative to input size, while space complexity tracks memory usage as input grows. We use Big O notation to express these upper limits, providing a clear picture of an algorithm's efficiency. Let's explore how to calculate this crucial metric!
Key Concepts
- Algorithm efficiency is determined by time and space complexity.
- Time complexity assesses execution time based on input size.
- Space complexity measures memory consumption as input size increases.
- Big O notation simplifies complexity analysis by focusing on growth rates.
- Optimizing both time and space complexity is key to efficient algorithms.

Table of Contents
- What is Time Complexity?
- What is Space Complexity?
- A Step-by-Step Guide to Calculating Algorithm Efficiency
- Step 1: Understanding the Algorithm
- Step 2: Analyzing Time Complexity
- Step 3: Analyzing Space Complexity
- Step 4: Simplifying the Complexity Expression
- Frequently Asked Questions
What is Time Complexity?
Time and space complexity are fundamental measures of algorithm efficiency. Time complexity quantifies the algorithm's execution time as a function of input size – essentially, its speed. Big O notation provides an upper bound on this growth rate. Common time complexities include:
- O(1): Constant time – execution time remains constant regardless of input size.
- O(log n): Logarithmic time – time grows logarithmically with input size.
- O(n): Linear time – time grows linearly with input size.
- O(n log n): Linearithmic time – a combination of linear and logarithmic growth.
- O(n2): Quadratic time – time grows proportionally to the square of the input size.
- O(2?): Exponential time – time doubles with each additional input element.
- O(n!): Factorial time – time grows factorially with input size.
What is Space Complexity?
Space complexity measures the memory an algorithm consumes as a function of input size. It reflects the algorithm's memory efficiency. Like time complexity, it's expressed using Big O notation. Common space complexities include:
- O(1): Constant space – memory usage remains fixed regardless of input size.
- O(n): Linear space – memory usage grows linearly with input size.
- O(n2): Quadratic space – memory usage grows proportionally to the square of the input size.
Analyzing both time and space complexity provides a comprehensive understanding of an algorithm's overall efficiency.
A Step-by-Step Guide to Calculating Algorithm Efficiency
Step 1: Understanding the Algorithm
- Define the Problem: Clearly state the algorithm's purpose and identify the input size (n), often the number of input elements.
- Identify Basic Operations: Determine the algorithm's core operations (comparisons, arithmetic, assignments, etc.).
Step 2: Analyzing Time Complexity
- Identify Key Operations: Focus on the most time-consuming operations.
- Count Operations: Determine how often each key operation is performed relative to input size (n).
Example:
<code>def example_algorithm(arr):
n = len(arr)
sum = 0
for i in range(n):
sum = arr[i]
return sum</code>
Explanation:
- Initialization (
sum = 0): O(1) - Loop (
for i in range(n)): O(n) - Inside Loop (
sum = arr[i]): O(1) per iteration, O(n) total
Expressing Time Complexity:
The overall time complexity is O(n).
Considering Best, Average, and Worst Cases:
Analyze the algorithm's performance under best-case, average-case, and worst-case scenarios.
Step 3: Analyzing Space Complexity
- Identify Memory Usage: Determine memory used by variables, data structures, and the call stack.
- Count Memory Usage: Analyze memory consumption relative to input size (n).
Example (same as above):
Space Complexity:
-
sum: O(1) -
n: O(1) -
arr: O(n)
The overall space complexity is O(n).
Step 4: Simplifying the Complexity Expression
- Ignore Lower-Order Terms: Focus on the term with the highest growth rate.
- Ignore Constant Coefficients: Big O focuses on growth trends, not precise values.
Conclusion
Calculating algorithm efficiency involves analyzing time and space complexity using Big O notation. By following these steps, you can systematically evaluate and optimize algorithms for various input sizes. Experience with diverse algorithms will enhance your understanding of this crucial computer science concept.
Frequently Asked Questions
Q1: How can I improve algorithm efficiency? A: Optimize logic, use efficient data structures, avoid redundancy, employ memoization/caching, and decompose problems into smaller, more efficiently solvable subproblems.
Q2: What's the difference between best, average, and worst-case time complexities? A: Best-case represents the fewest steps, average-case the expected performance, and worst-case the maximum number of steps.
Q3: What is algorithm efficiency? A: Algorithm efficiency refers to how effectively an algorithm uses time and space resources.
Q4: What is Big O notation? A: Big O notation describes the upper bound of an algorithm's runtime or space requirements in the worst case, providing an asymptotic analysis of efficiency.
The above is the detailed content of How to Calculate Algorithm Efficiency?. For more information, please follow other related articles on the PHP Chinese website!

Hot AI Tools

Undress AI Tool
Undress images for free

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Clothoff.io
AI clothes remover

Video Face Swap
Swap faces in any video effortlessly with our completely free AI face swap tool!

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 1795
1795
 16
16
 1744
1744
 56
56
 1593
1593
 29
29
 1475
1475
 72
72
 267
267
 587
587
 AI Investor Stuck At A Standstill? 3 Strategic Paths To Buy, Build, Or Partner With AI Vendors
Jul 02, 2025 am 11:13 AM
AI Investor Stuck At A Standstill? 3 Strategic Paths To Buy, Build, Or Partner With AI Vendors
Jul 02, 2025 am 11:13 AM
Investing is booming, but capital alone isn’t enough. With valuations rising and distinctiveness fading, investors in AI-focused venture funds must make a key decision: Buy, build, or partner to gain an edge? Here’s how to evaluate each option—and pr
 AGI And AI Superintelligence Are Going To Sharply Hit The Human Ceiling Assumption Barrier
Jul 04, 2025 am 11:10 AM
AGI And AI Superintelligence Are Going To Sharply Hit The Human Ceiling Assumption Barrier
Jul 04, 2025 am 11:10 AM
Let’s talk about it. This analysis of an innovative AI breakthrough is part of my ongoing Forbes column coverage on the latest in AI, including identifying and explaining various impactful AI complexities (see the link here). Heading Toward AGI And
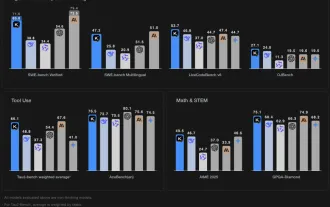 Kimi K2: The Most Powerful Open-Source Agentic Model
Jul 12, 2025 am 09:16 AM
Kimi K2: The Most Powerful Open-Source Agentic Model
Jul 12, 2025 am 09:16 AM
Remember the flood of open-source Chinese models that disrupted the GenAI industry earlier this year? While DeepSeek took most of the headlines, Kimi K1.5 was one of the prominent names in the list. And the model was quite cool.
 Future Forecasting A Massive Intelligence Explosion On The Path From AI To AGI
Jul 02, 2025 am 11:19 AM
Future Forecasting A Massive Intelligence Explosion On The Path From AI To AGI
Jul 02, 2025 am 11:19 AM
Let’s talk about it. This analysis of an innovative AI breakthrough is part of my ongoing Forbes column coverage on the latest in AI, including identifying and explaining various impactful AI complexities (see the link here). For those readers who h
 Grok 4 vs Claude 4: Which is Better?
Jul 12, 2025 am 09:37 AM
Grok 4 vs Claude 4: Which is Better?
Jul 12, 2025 am 09:37 AM
By mid-2025, the AI “arms race” is heating up, and xAI and Anthropic have both released their flagship models, Grok 4 and Claude 4. These two models are at opposite ends of the design philosophy and deployment platform, yet they
 Chain Of Thought For Reasoning Models Might Not Work Out Long-Term
Jul 02, 2025 am 11:18 AM
Chain Of Thought For Reasoning Models Might Not Work Out Long-Term
Jul 02, 2025 am 11:18 AM
For example, if you ask a model a question like: “what does (X) person do at (X) company?” you may see a reasoning chain that looks something like this, assuming the system knows how to retrieve the necessary information:Locating details about the co
 Batch Processing vs Mini-Batch Training in Deep Learning
Jun 30, 2025 am 09:46 AM
Batch Processing vs Mini-Batch Training in Deep Learning
Jun 30, 2025 am 09:46 AM
Deep learning has revolutionised the AI field by allowing machines to grasp more in-depth information within our data. Deep learning has been able to do this by replicating how our brain functions through the logic of neuron syna
 This Startup Built A Hospital In India To Test Its AI Software
Jul 02, 2025 am 11:14 AM
This Startup Built A Hospital In India To Test Its AI Software
Jul 02, 2025 am 11:14 AM
Clinical trials are an enormous bottleneck in drug development, and Kim and Reddy thought the AI-enabled software they’d been building at Pi Health could help do them faster and cheaper by expanding the pool of potentially eligible patients. But the