Key Takeaways

• Diagramme sind mathematische Konstrukte, die zum Modellieren von Beziehungen zwischen Schlüssel-/Wertpaaren verwendet werden, und haben zahlreiche reale Anwendungen wie Netzwerkoptimierung, Verkehrsrouting und soziale Netzwerkanalyse. Sie bestehen aus Scheitelpunkten (Knoten) und Kanten (Zeilen), die sie verbinden, die gerichtet oder ungerichtet und gewichtet oder ungewichtet sind.
• Diagramme k?nnen auf zwei Arten dargestellt werden: als Adjazenzmatrix oder Adjazenzliste. Die Adjazenzlisten sind platz effizienter, insbesondere für sp?rliche Graphen, bei denen die meisten Eckpaare nicht verbunden sind, w?hrend Adjazenzmatrizen schnellere Lookups erm?glichen.
• Eine gemeinsame Anwendung der Graphentheorie findet die geringste Anzahl von Hopfen (d. H. Der kürzeste Weg) zwischen zwei beliebigen Knoten. Dies kann mithilfe der Breite-First-Suche erreicht werden, bei der die Grafikpegel durch einen festgelegten Stammknoten durch die Grafikniveau durchquert wird. Dieser Prozess erfordert die Aufrechterhaltung einer Warteschlange von nicht besuchten Knoten.
Der Algorithmus von
• Dijkstra wird h?ufig verwendet, um den kürzesten oder optimalen Pfad zwischen zwei beliebigen Knoten in einem Diagramm zu finden. Dies beinhaltet die Untersuchung jeder Kante zwischen allen m?glichen Scheitelpunktpaaren, die vom Quellknoten beginnen, und die Aufrechterhaltung eines aktualisierten Satzes von Scheitelpunkten mit dem kürzesten Gesamtabstand, bis der Zielknoten erreicht ist.

In einem meiner vorherigen Artikel habe ich Sie in die Baumdatenstruktur eingeführt. Jetzt m?chte ich eine verwandte Struktur untersuchen - die Grafik. Diagramme haben eine Reihe realer Anwendungen wie Netzwerkoptimierung, Verkehrsrouting und soziale Netzwerkanalyse. Die PageRank von Google, Facebooks Graphsuche sowie Empfehlungen von Amazon und Netflix sind einige Beispiele für graphgesteuerte Anwendungen. In diesem Artikel werde ich zwei h?ufige Probleme untersuchen, bei denen Grafiken verwendet werden-die geringste Anzahl von Hops und kürzesten Path-Problemen. Ein Diagramm ist ein mathematisches Konstrukt, das verwendet wird, um die Beziehungen zwischen Schlüssel-/Wertpaaren zu modellieren. Ein Diagramm umfasst einen Satz -Keitel (Knoten) und eine beliebige Anzahl von -Kunden (Zeilen), die sie verbinden. Diese Kanten k?nnen gerichtet oder ungerichtet werden. Eine gerichtete Kante ist einfach eine Kante zwischen zwei Eckpunkten, und die Kante A → B wird nicht dasselbe wie B → A betrachtet. Eine ungerichtete Kante hat keine Ausrichtung oder Richtung; Edge A-B entspricht B-A. Eine Baumstruktur, über die wir das letzte Mal gelernt haben, kann als eine Art ungerichteter Graphen angesehen werden, wobei jeder Scheitelpunkt durch einen einfachen Pfad mit mindestens einem anderen Scheitelpunkt verbunden ist. Diagramme k?nnen auch gewichtet oder ungewichtet werden. Ein gewichtetes Diagramm oder ein Netzwerk ist eines, bei dem jeder seiner Kanten ein Gewicht oder einen Kostenwert zugeordnet wird. Gewichtete Diagramme werden üblicherweise zur Bestimmung des optimalsten, am zweckm??igsten oder dem niedrigsten ?Kosten“ zwischen zwei Punkten. Die Fahranleitung von Googlemap ist ein Beispiel, das gewichtete Graphen verwendet.

die geringste Anzahl von Hops

Eine gemeinsame Anwendung der Graphentheorie besteht darin, die geringste Anzahl von Hopfen zwischen zwei beliebigen Knoten zu finden. Wie bei B?umen k?nnen Diagramme auf zwei Arten durchquert werden: Tiefen- oder Breite. Wir haben im vorherigen Artikel die Suche in der Tiefe zuerst behandelt. Schauen wir uns also die Breite der ersten Suche an. Betrachten Sie die folgende Grafik:

Nehmen wir zum Einfachheit halber an, dass der Diagramm ungerichtet ist - das hei?t, die Kanten in eine beliebige Richtung sind identisch. Unsere Aufgabe ist es, die geringste Anzahl von Hopfen zwischen zwei beliebigen Knoten zu finden. Bei einer breiten Suche beginnen wir am Root-Knoten (oder an jedem als Wurzel bezeichneten Knoten) und arbeiten uns auf der Ebene auf die Baumebene hinunter. Dazu ben?tigen wir eine Warteschlange, um eine Liste nicht besuchter Knoten zu verwalten, damit wir sie nach jeder Ebene zurückverfolgen und verarbeiten k?nnen. Der allgemeine Algorithmus sieht so aus:

1. Create a queue
2. Enqueue the root node and mark it as visited
3. While the queue is not empty do:
  3a. dequeue the current node
  3b. if the current node is the one we're looking for then stop
  3c. else enqueue each unvisited adjacent node and mark as visited

Aber woher wissen wir, welche Knoten benachbart sind, geschweige denn nicht besucht, ohne zuerst die Grafik zu durchqueren? Dies bringt uns zu dem Problem, wie eine Diagrammdatenstruktur modelliert werden kann.

Darstellung des Diagramms

Es gibt im Allgemeinen zwei M?glichkeiten, ein Diagramm darzustellen: entweder als Adjazenzmatrix oder als Adjazenzliste. Die obige Grafik, die als Adjazenzliste dargestellt wird, sieht Folgendes aus: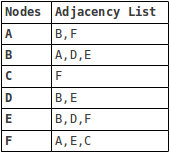

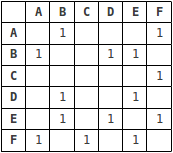
Das als Matrix dargestellte Grafik sieht so aus, wobei 1 eine ?Inzidenz“ einer Kante zwischen 2 Scheitelpunkten angibt:

Adjazenzlisten sind platzeffizienter, insbesondere für sp?rliche Graphen, in denen die meisten Eckpaare nicht verbunden sind, w?hrend Adjazenzmatrizen schnellere Lookups erm?glichen. Letztendlich h?ngt die Auswahl der Darstellung davon ab, welche Art von Grafikvorg?ngen wahrscheinlich erforderlich sind. Verwenden wir eine Adjazenzliste, um die Grafik darzustellen:

1. Create a queue
2. Enqueue the root node and mark it as visited
3. While the queue is not empty do:
  3a. dequeue the current node
  3b. if the current node is the one we're looking for then stop
  3c. else enqueue each unvisited adjacent node and mark as visited

Und nun sehen wir sehen, wie die Implementierung des allgemeinen Breit-First-Suchalgorithmus aussieht:

<span><span><?php
</span></span><span><span>$graph = array(
</span></span><span>  <span>'A' => array('B', 'F'),
</span></span><span>  <span>'B' => array('A', 'D', 'E'),
</span></span><span>  <span>'C' => array('F'),
</span></span><span>  <span>'D' => array('B', 'E'),
</span></span><span>  <span>'E' => array('B', 'D', 'F'),
</span></span><span>  <span>'F' => array('A', 'E', 'C'),
</span></span><span><span>);</span></span>

Wenn wir die folgenden Beispiele ausführen, bekommen wir:

<span><span><?php
</span></span><span><span>class Graph
</span></span><span><span>{
</span></span><span>  <span>protected $graph;
</span></span><span>  <span>protected $visited = array();
</span></span><span>
</span><span>  <span>public function __construct($graph) {
</span></span><span>    <span>$this->graph = $graph;
</span></span><span>  <span>}
</span></span><span>
</span><span>  <span>// find least number of hops (edges) between 2 nodes
</span></span><span>  <span>// (vertices)
</span></span><span>  <span>public function breadthFirstSearch($origin, $destination) {
</span></span><span>    <span>// mark all nodes as unvisited
</span></span><span>    <span>foreach ($this->graph as $vertex => $adj) {
</span></span><span>      <span>$this->visited[$vertex] = false;
</span></span><span>    <span>}
</span></span><span>
</span><span>    <span>// create an empty queue
</span></span><span>    <span>$q = new SplQueue();
</span></span><span>
</span><span>    <span>// enqueue the origin vertex and mark as visited
</span></span><span>    <span>$q->enqueue($origin);
</span></span><span>    <span>$this->visited[$origin] = true;
</span></span><span>
</span><span>    <span>// this is used to track the path back from each node
</span></span><span>    <span>$path = array();
</span></span><span>    <span>$path[$origin] = new SplDoublyLinkedList();
</span></span><span>    <span>$path[$origin]->setIteratorMode(
</span></span><span>      <span>SplDoublyLinkedList<span>::</span>IT_MODE_FIFO|SplDoublyLinkedList<span>::</span>IT_MODE_KEEP
</span></span><span>    <span>);
</span></span><span>
</span><span>    <span>$path[$origin]->push($origin);
</span></span><span>
</span><span>    <span>$found = false;
</span></span><span>    <span>// while queue is not empty and destination not found
</span></span><span>    <span>while (!$q->isEmpty() && $q->bottom() != $destination) {
</span></span><span>      <span>$t = $q->dequeue();
</span></span><span>
</span><span>      <span>if (!empty($this->graph[$t])) {
</span></span><span>        <span>// for each adjacent neighbor
</span></span><span>        <span>foreach ($this->graph[$t] as $vertex) {
</span></span><span>          <span>if (!$this->visited[$vertex]) {
</span></span><span>            <span>// if not yet visited, enqueue vertex and mark
</span></span><span>            <span>// as visited
</span></span><span>            <span>$q->enqueue($vertex);
</span></span><span>            <span>$this->visited[$vertex] = true;
</span></span><span>            <span>// add vertex to current path
</span></span><span>            <span>$path[$vertex] = clone $path[$t];
</span></span><span>            <span>$path[$vertex]->push($vertex);
</span></span><span>          <span>}
</span></span><span>        <span>}
</span></span><span>      <span>}
</span></span><span>    <span>}
</span></span><span>
</span><span>    <span>if (isset($path[$destination])) {
</span></span><span>      <span>echo "<span><span>$origin</span> to <span>$destination</span> in "</span>, 
</span></span><span>        <span>count($path[$destination]) - 1,
</span></span><span>        <span>" hopsn";
</span></span><span>      <span>$sep = '';
</span></span><span>      <span>foreach ($path[$destination] as $vertex) {
</span></span><span>        <span>echo $sep, $vertex;
</span></span><span>        <span>$sep = '->';
</span></span><span>      <span>}
</span></span><span>      <span>echo "n";
</span></span><span>    <span>}
</span></span><span>    <span>else {
</span></span><span>      <span>echo "No route from <span><span>$origin</span> to <span>$destinationn</span>"</span>;
</span></span><span>    <span>}
</span></span><span>  <span>}
</span></span><span><span>}</span></span>

Wenn wir einen Stapel anstelle einer Warteschlange verwendet hatten, wird der Traversal zu einer Tiefensuche.

Finden Sie den kürzesten Pfad

Ein weiteres h?ufiges Problem ist es, den optimalsten Weg zwischen zwei beliebigen Knoten zu finden. Früher erw?hnte ich die Fahranleitung von Googlemap als Beispiel dafür. Weitere Anwendungen sind Planungsreisen, Stra?enverkehrsmanagement und Zug-/Busplanung. Einer der berühmtesten Algorithmen, die dieses Problem angehen, wurde 1959 von einem 29-j?hrigen Informatiker namens Edsger W. Dijkstra erfunden. Im Allgemeinen umfasst die L?sung von Dijkstra die Untersuchung jeder Kante zwischen allen m?glichen Scheitelpunktpaaren, die vom Quellknoten beginnen, und die Aufrechterhaltung eines aktualisierten Satzes von Scheitelpunkten mit kürzester Gesamtentfernung, bis der Zielknoten erreicht ist oder nicht erreicht ist, je nachdem, welcher Fall auch nicht sein kann. Es gibt verschiedene M?glichkeiten, die L?sung zu implementieren, und in der Tat wurden über Jahre nach 1959 viele Verbesserungen - unter Verwendung von Minheaps, Priorit?tsquellen und Fibonacci -Haufen - an Dijkstras ursprünglicher Algorithmus gemacht. Einige verbesserte Leistung, w?hrend andere so konzipiert waren, dass sie M?ngel in der Dijkstra -L?sung behandeln, da sie nur mit positiv gewichteten Graphen arbeitete (bei denen die Gewichte positive Werte sind). Hier ist ein Beispiel für eine (positive) gewichtete Grafik: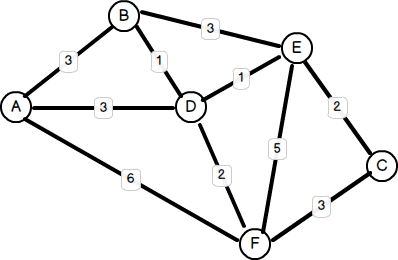

Wir k?nnen diese Grafik wie folgt als Adjazenzliste darstellen:

1. Create a queue
2. Enqueue the root node and mark it as visited
3. While the queue is not empty do:
  3a. dequeue the current node
  3b. if the current node is the one we're looking for then stop
  3c. else enqueue each unvisited adjacent node and mark as visited

Und hier finden Sie eine Implementierung mit einem Priorit?tsqueue, um eine Liste aller ?nicht optimierten“ Scheitelpunkte beizubehalten:

<span><span><?php
</span></span><span><span>$graph = array(
</span></span><span>  <span>'A' => array('B', 'F'),
</span></span><span>  <span>'B' => array('A', 'D', 'E'),
</span></span><span>  <span>'C' => array('F'),
</span></span><span>  <span>'D' => array('B', 'E'),
</span></span><span>  <span>'E' => array('B', 'D', 'F'),
</span></span><span>  <span>'F' => array('A', 'E', 'C'),
</span></span><span><span>);</span></span>

Wie Sie sehen k?nnen, ist die L?sung von Dijkstra einfach eine Variation der Breite-First-Suche! Das Ausführen der folgenden Beispiele liefert die folgenden Ergebnisse:

<span><span><?php
</span></span><span><span>class Graph
</span></span><span><span>{
</span></span><span>  <span>protected $graph;
</span></span><span>  <span>protected $visited = array();
</span></span><span>
</span><span>  <span>public function __construct($graph) {
</span></span><span>    <span>$this->graph = $graph;
</span></span><span>  <span>}
</span></span><span>
</span><span>  <span>// find least number of hops (edges) between 2 nodes
</span></span><span>  <span>// (vertices)
</span></span><span>  <span>public function breadthFirstSearch($origin, $destination) {
</span></span><span>    <span>// mark all nodes as unvisited
</span></span><span>    <span>foreach ($this->graph as $vertex => $adj) {
</span></span><span>      <span>$this->visited[$vertex] = false;
</span></span><span>    <span>}
</span></span><span>
</span><span>    <span>// create an empty queue
</span></span><span>    <span>$q = new SplQueue();
</span></span><span>
</span><span>    <span>// enqueue the origin vertex and mark as visited
</span></span><span>    <span>$q->enqueue($origin);
</span></span><span>    <span>$this->visited[$origin] = true;
</span></span><span>
</span><span>    <span>// this is used to track the path back from each node
</span></span><span>    <span>$path = array();
</span></span><span>    <span>$path[$origin] = new SplDoublyLinkedList();
</span></span><span>    <span>$path[$origin]->setIteratorMode(
</span></span><span>      <span>SplDoublyLinkedList<span>::</span>IT_MODE_FIFO|SplDoublyLinkedList<span>::</span>IT_MODE_KEEP
</span></span><span>    <span>);
</span></span><span>
</span><span>    <span>$path[$origin]->push($origin);
</span></span><span>
</span><span>    <span>$found = false;
</span></span><span>    <span>// while queue is not empty and destination not found
</span></span><span>    <span>while (!$q->isEmpty() && $q->bottom() != $destination) {
</span></span><span>      <span>$t = $q->dequeue();
</span></span><span>
</span><span>      <span>if (!empty($this->graph[$t])) {
</span></span><span>        <span>// for each adjacent neighbor
</span></span><span>        <span>foreach ($this->graph[$t] as $vertex) {
</span></span><span>          <span>if (!$this->visited[$vertex]) {
</span></span><span>            <span>// if not yet visited, enqueue vertex and mark
</span></span><span>            <span>// as visited
</span></span><span>            <span>$q->enqueue($vertex);
</span></span><span>            <span>$this->visited[$vertex] = true;
</span></span><span>            <span>// add vertex to current path
</span></span><span>            <span>$path[$vertex] = clone $path[$t];
</span></span><span>            <span>$path[$vertex]->push($vertex);
</span></span><span>          <span>}
</span></span><span>        <span>}
</span></span><span>      <span>}
</span></span><span>    <span>}
</span></span><span>
</span><span>    <span>if (isset($path[$destination])) {
</span></span><span>      <span>echo "<span><span>$origin</span> to <span>$destination</span> in "</span>, 
</span></span><span>        <span>count($path[$destination]) - 1,
</span></span><span>        <span>" hopsn";
</span></span><span>      <span>$sep = '';
</span></span><span>      <span>foreach ($path[$destination] as $vertex) {
</span></span><span>        <span>echo $sep, $vertex;
</span></span><span>        <span>$sep = '->';
</span></span><span>      <span>}
</span></span><span>      <span>echo "n";
</span></span><span>    <span>}
</span></span><span>    <span>else {
</span></span><span>      <span>echo "No route from <span><span>$origin</span> to <span>$destinationn</span>"</span>;
</span></span><span>    <span>}
</span></span><span>  <span>}
</span></span><span><span>}</span></span>

Zusammenfassung

In diesem Artikel habe ich die Grundlagen der Graphentheorie, zwei M?glichkeiten zur Darstellung von Grafiken und zwei grundlegende Probleme in der Anwendung der Graphentheorie eingeführt. Ich habe Ihnen gezeigt, wie eine Breite-First-Suche verwendet wird, um die geringste Anzahl von Hopfen zwischen zwei beliebigen Knoten zu finden und wie Dijkstra-L?sung verwendet wird, um den kürzesten Weg zwischen zwei beliebigen Knoten zu finden. Bild über Fotolien

h?ufig gestellte Fragen (FAQs) zu Grafiken in Datenstrukturen

Was ist der Unterschied zwischen einem Diagramm und einem Baum in Datenstrukturen? Ein Baum ist eine Art Grafik, aber nicht alle Grafiken sind B?ume. Ein Baum ist ein verbundenes Diagramm ohne Zyklen. Es hat eine hierarchische Struktur mit einem Wurzelknoten und einem untergeordneten Knoten. Jeder Knoten in einem Baum hat einen einzigartigen Weg von der Wurzel. Andererseits kann ein Diagramm Zyklen haben und seine Struktur ist komplexer. Es kann verbunden oder getrennt werden und Knoten k?nnen mehrere Pfade zwischen sich haben.

Wie werden Grafiken in Datenstrukturen dargestellt? Liste. Eine Adjazenzmatrix ist ein 2D -Array der Gr??e V x V, wobei V die Anzahl der Scheitelpunkte im Diagramm ist. Wenn zwischen den Scheitelpunkten I und J eine Kante gibt, ist die Zelle an der Kreuzung von Zeile I und Spalte J 1, ansonsten 0. Eine Adjazenzliste ist ein Array von verknüpften Listen. Der Index des Arrays repr?sentiert einen Scheitelpunkt und jedes Element in seiner verknüpften Liste der anderen Scheitelpunkte, die mit dem Scheitelpunkt eine Kante bilden. sind verschiedene Arten von Grafiken in Datenstrukturen. Ein einfaches Diagramm ist ein Diagramm ohne Schleifen und nicht mehr als eine Kante zwischen zwei Eckpunkten. Ein Multigraph kann mehrere Kanten zwischen Scheitelpunkten haben. Ein komplettes Diagramm ist ein einfaches Diagramm, in dem jedes Eckpaar durch eine Kante verbunden ist. Ein gewichteter Diagramm weist jeder Kante ein Gewicht zu. Ein gerichteter Diagramm (oder Digraph) hat Kanten mit einer Richtung. Die Kanten zeigen von einem Scheitelpunkt zum anderen.

Welche Anwendungen von Grafiken in der Informatik werden in zahlreichen Anwendungen in der Informatik

Diagramme verwendet. Sie werden in sozialen Netzwerken verwendet, um Verbindungen zwischen Menschen darzustellen. Sie werden im Web -Crawling verwendet, um Webseiten zu besuchen und einen Suchindex zu erstellen. Sie werden in Netzwerk -Routing -Algorithmen verwendet, um den besten Weg zwischen zwei Knoten zu finden. Sie werden in Biologie verwendet, um biologische Netzwerke zu modellieren und zu analysieren. Sie werden auch in Computergrafik- und Physik-Simulationen verwendet. (BFS). DFS erforscht vor dem Backtracking so weit wie m?glich an jedem Zweig. Es verwendet eine Stapeldatenstruktur. BFS untersucht alle Scheitelpunkte in der gegenw?rtigen Tiefe, bevor er zur n?chsten Ebene geht. Es verwendet eine Warteschlangendatenstruktur. Jeder Schlüssel im HashMap ist ein Scheitelpunkt und sein Wert ist eine verknüpfte Liste, die die Scheitelpunkte enth?lt, an die er angeschlossen ist. in zwei disjunkte S?tze unterteilt werden, so dass jede Kante einen Scheitelpunkt in einem Set an einen Scheitelpunkt im anderen Satz verbindet. Kein Kanten verbindet Scheitelpunkte innerhalb desselben Satzes.

Was ist ein Untergraphen? Es hat einige (oder alle) Eckpunkte des Originalgrafiks und einige (oder alle) Kanten des Originalgraps.

Was ist ein Zyklus in einem Diagramm? Ein Pfad, der am selben Scheitelpunkt beginnt und endet und mindestens eine Kante hat.

Was ist ein Pfad in einem Diagramm? von Konsekutive Eckpunkte sind durch eine Kante verbunden.

Das obige ist der detaillierte Inhalt vonPHP Master | Datenstrukturen für PHP -Entwickler: Diagramme. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!